AOJ 2386: Sightseeing Tour

はじめに

• ハマりポイントとして、リンク先のPDFの1問目がこの問題ではありません。PDFを下にスクロールする必要があります。ここでめっちゃハマりました。

問題文幻想郷訳

• 原文: http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2386

幻想郷はN箇所の観光地がある。 現在、どの2つの観光地も道でつながっている。 しかし、幻想郷神主ZUNは、すべての道を一方通行にしたいと思っている。 観光地iと観光地jをつなぐ道を、iからjへの一方通行にするためには、 円かかる。 神主はこの費用をなるべく節約したいと考えている。

一方で、幻想郷にとっては観光も重要な産業である。 幻想郷にはバスはないが、すべての観光地を回るツアーがある。 そのため、すべての観光地をちょうど1回づつまわるルートが必要である。 ただし、スタートの観光地とゴールの観光地は同じでなくてもよい。 あなたは最も少ない費用で、このような条件をみたす一方通行化の方法を提案して欲しい。

方針と証明

• 完全グラフの無向グラフを有向グラフに変換して、オイラー閉路の存在を保ちつつ、コストが最小となるように道を作る。
• 巡回サラリーマン問題かなーと思ったが、そんなに難しく考えなくても良かった。

完全グラフ（どの2点完もノードを持つ）の有効グラフはかならずオイラー閉路を持つという性質があります。つまり、[tex: C{i,j} と C{j,i}] のうちひたすら小さい方を選んで道を作っていけばいいということになります。

証明

まず、n=2のとき、この事実は明らかです。

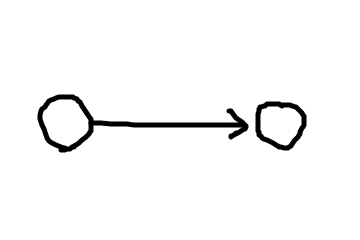
では、nのときオイラー閉路を持つとします。ここに新しくノードを追加して、n+1の場合を考えてみましょう。

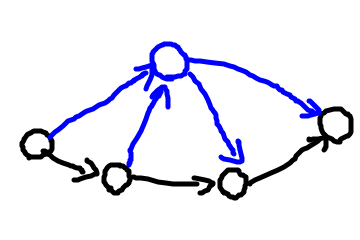
黒がもともと存在していたオイラー閉路であったとして、青のノードを追加してみました。完全グラフなので、もともとあったすべての閉路上にエッジが貼られています。なので、もともとの閉路から青いノードに寄り道して、またもともとも閉路に戻れるような道が必ず存在します。

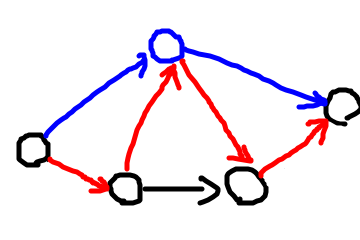
赤いのが新しい閉路ですね。じゃあもしこうだったらどうなるんだ

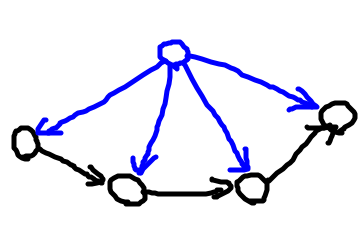
この場合は、青いノードからスタートすれば閉路が存在しますね。そんなわけで、一方通行の向きはどのようにとっても良いわけですね。ということはコストが安い方を選ぶほうがいいわけです。簡単ですね。

実装

• http://judge.u-aizu.ac.jp/onlinejudge/review.jsp?rid=1375161

class Main extends MyUtil{
    public static void main(String[] args) throws Exception{
        // 入力には独自クラスを使っている
        int n = readInt();
        int[][] c = new int[n][];
        for (int i = 0; i < n; i++) {
            c[i] = readIntMap();
        }
        
        long ans = 0;
        for(int i = 0; i < n; i++){
            for(int j = 0; j < i; j++){
                ans += Math.min(c[i][j], c[j][i]);
            }
        }
        System.out.println(ans);
    }
}

参考