AOJ 2021: Princess in Danger （お姫様の危機）

どうも、yoshikyotoです。この問題、問題文が分かりづらく、曖昧さを含んでいる上に、Sample Input もおかしかったので苦労してしまいました。まずはそこから解決していこうと思います。

問題: http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2021

問題文の曖昧さについて - 入力形式

冷凍施設がある街が、首都とゴール以外に無いケースがあります（l = 0 のケース）。この場合、Sample Input では、そもそも冷凍施設についての行が消えてしまっています。しかし、テストケースでは、冷凍施設にについての行は、改行のみを含む1行が存在しています。C++の std::cin や、Javaの Scanner を使っていればあまり問題になりませんが、Javaで BufferedReader で readLine() とかしているとハマる可能性があります。注意してください。

解法

スタートとゴールは冷凍施設がある街であるとみなします。

1. ワーシャルフロイド法で任意の2つ街の最短距離を求めます。

ワーシャルフロイドとはどういうアルゴリズムか、以下のようなグラフがあったとします。

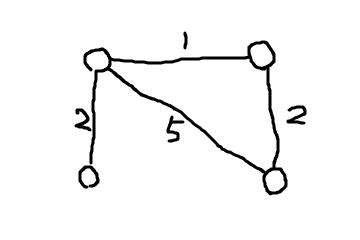
このグラフを以下のように更新するのがワーシャルフロイドです。

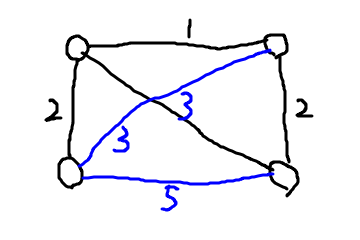
つまり、任意の2点間のエッジにその2点間の最小距離が入るようにグラフを更新します。

2. 冷凍できない街は消す

上のグラフに対して、下の図の青いノードが冷凍出来る街、赤いS,Gがスタート、ゴールだとすると、冷凍できない街とそこにくっついているエッジの情報は消してしまいます。

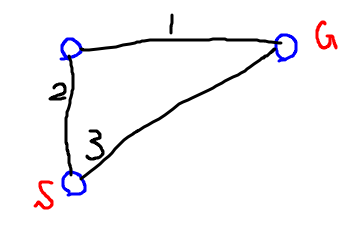
今回の問題の場合、冷凍施設を持っている街同士の距離だけが重要となります。それ以外の街はただの道とみなしても問題ありません。ワーシャルフロイドを行ってから冷凍施設のない街を消すことで、冷凍施設の無い街はただの道であるとみなしています。

3. 間に合わないエッジは消す

さて、ここで M = 2 であったとします。ここで、距離がMより大きいエッジは削除してしまいます。

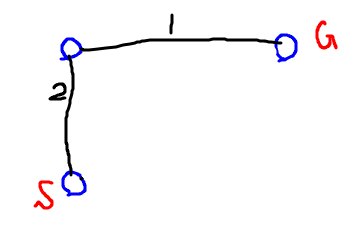
これで、スタートからゴールまでがつながっていた場合は、血液を運ぶことができます。繋がっていない場合は Help! です。

4. 時間を求める

スタートからゴールまでの最短距離を求めます。もいっちょワーシャルフロイドをしましょう。

今回の場合は、たまたまひとつ前のグラフと全く同じになってしまいましたが、場合によっては違うグラフになることもあります。このグラフが意味していることは、「スタートからゴールまで血液を運ぶことが保証されていて、冷凍時間を除いたら3分間で到達できる」ということです。ここからどうやって時間を求めるのでしょうか。

実はこれは簡単です。今回、M=2としていますので、スタートの時点でタイムリミットが2分です。運ぶ時間は3分なので、どこかで1分冷凍しなければなりません。よって運搬3分、冷凍1分で合計4分かかることになります。もしM=5であったとしたら、冷凍しなくて済むので運搬の3分のみとなります。

実装

説明が長くてわかりづらかったかもしれませんが、なんとなく分かっていただけたでしょうか？以下ソースコードとなります。ワーシャルフロイドは見ての通り3重ループなので、ノード数³ かかります。今回はn=100なのでなんとか間に合います。

class Main extends MyIO {
    public static void main(String[] args) throws Exception {
        while(true) {
            // 入出力には自作クラスを使用しています。
            int n = readIntMap(0);    // 街の数
            int m = readIntMap(1);    // 制限時間
            int l = readIntMap(2);    // 冷凍施設のある街の数
            int k = readIntMap(3);    // 道路の数
            int a = readIntMap(4);    // スタート
            int h = readIntMap(5);    // ゴール
            if(n+m+l+k+a+h == 0) break;
            
            int[][] g = new int[n][n];
            
            boolean[] canFreeze = new boolean[n];
            canFreeze[a] = true;
            canFreeze[h] = true;
            if(l != 0){
                int list[] = readIntMap();
                for (int i = 0; i < l; i++) {
                    canFreeze[list[i]] = true;
                }
            }else{
                readLine();
            }
            
            for (int i = 0; i < k; i++) {
                int x = readIntMap(0);
                int y = readIntMap(1);
                int t = readIntMap(2);
                g[x][y] = t;
                g[y][x] = t;
            }
            
            // ワーシャルフロイドで最短距離を求める
            warshallFloyd(g, n);
            
            // 凍らせられない街のみにする
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if(!canFreeze[i] || !canFreeze[j]){
                        g[i][j] = 0;
                    }
                }
            }
            
            // 届かないエッジを除く
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if(g[i][j] > m){
                        g[i][j] = 0;
                    }
                }
            }
            
            // この状態でもう一回ワーシャルフロイド
            warshallFloyd(g, n);
            
            if(g[a][h] == 0){
                System.out.println("Help!");
            }else if(g[a][h] <= m){
                System.out.println(g[a][h]);
            }else{
                System.out.println(g[a][h] * 2 - m);
            }
        }
    }
    
    /**
    * ワーシャルフロイド法
    * コストが0だとエッジがないとみなされる版
    */
    static void warshallFloyd(int[][] g, int n){
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if(i == j) continue;
                    if(g[i][k] == 0 || g[k][j] == 0) continue;
                    if(g[i][j] == 0) {
                        g[i][j] = g[i][k] + g[k][j]; 
                    } else {
                        g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);
                    }
                }
            }
        }
    }
}