
問4 次の表は,ある高校の定期試験における英語と数学の結果である。
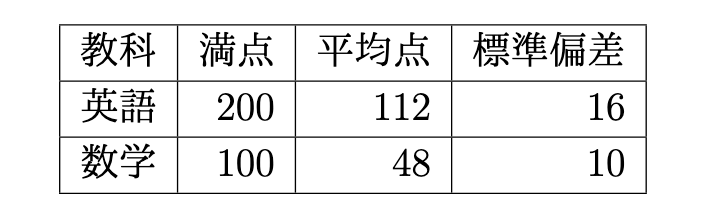
(1) 全員の数学の点数に10点を加算することとした。その際,100点を超えた人はいないものとする。このときの数学の点数の平均点と標準偏差の組合せとして,次の1~5のうちから適切なものを一つ選べ。
平均点は10点上がる。
標準偏差 = √分散 である。分散は「みんながどれくらい平均と離れているか」を表す値であり、標準偏差もほぼ同じ意味を持つ。
今回、全員の点数が10点加算されたため、「みんながどれくらい平均と離れているか」は変化しない。よって、標準偏差は変化しない。
(2)上の表の英語と数学の点数を,それぞれ定数倍して50点満点に換算したとき,次のI~IIIの記述を考えた。
I.英語の方が数学よりも平均点が高い。
50点満点にしたとき、英語は1/4、数学は1/2の点数になる。平均点もそれぞれ 1/4, 1/2 されるので、28点, 24点で、英語のほうが平均点は高い。
II.英語の方が数学よりも分散が大きい。
標準偏差 = √分散 のため、「分散が大きい」は、「標準偏差が大きい」と同じことになる。
標準偏差は、分散と同様に、「みんながどれくらい平均と離れているか」を表す値である。点数が1/4や1/2に圧縮されると、平均との距離は近くなるので、標準偏差や分散は小さくなる。
分散は、平均との二乗平均誤差なので、全員の点数が 1/4 になった場合、分散は (1/4)2 になる。
標準偏差は、√分散。全員の点数が 1/4 になった場合、分散は (1/4)2 になり、標準偏差は 1/4 になる。
英語の点数が 1/4 になるので、標準偏差も 1/4 になり、標準偏差は4。数学は1/2なので、標準偏差は5。数学の方が標準偏差は大きくなるので、分散は数学の方が大きい。
III.英語の方が数学よりも変動係数が大きい。
変動係数は、 標準偏差 / 平均値 である。これい基づいて計算すると、英語の方が変動係数が大きくなる。
標準偏差は、点数の圧縮等により変化する問題点がある。200点満点の英語のほうが、100点満点の数学より、標準偏差が大きくなりやすいのである。
変動係数は、標準偏差を平均で割ることにより、点数の圧縮などの影響を受けなくなる。点数を50点満点に圧縮しても、変動係数の値が変わらないことが、変動係数の特徴である。